最优化理论与方法-无约束优化

无约束优化

• 无约束优化问题

  • 无约束优化问题是指在没有任何限制条件下，最小化一个依赖于实变量的目标函数：

    $$\min_{x} f(x)$$

    其中 $x \in \mathbb{R}^n$（$n \geq 1$）是一个实向量，函数 $f: \mathbb{R}^n \to \mathbb{R}$ 通常是光滑的（例如连续可微）。

• 什么是一个解？

  • 全局最小值点：
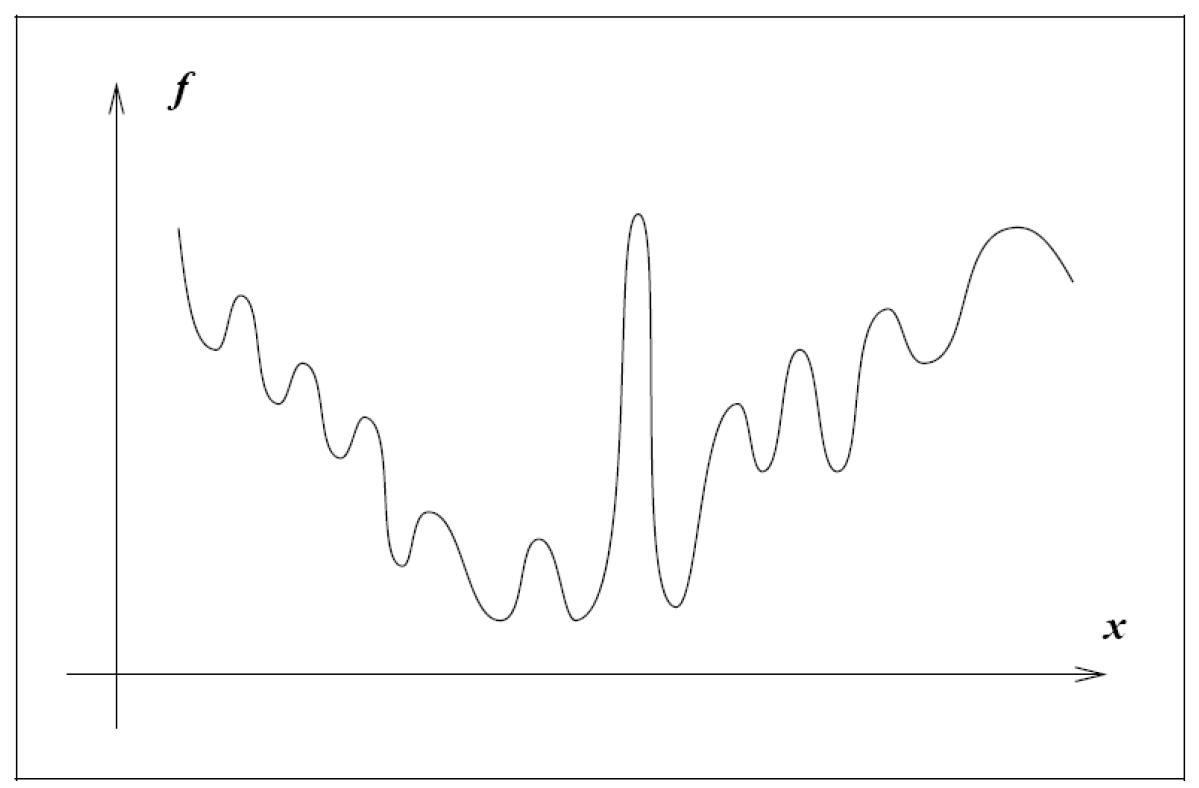
    点 $x^*$ 称为函数 $f$ 的全局最小值点，如果

    $$f(x^*) \leq f(x), \quad \forall\, x \in \mathbb{R}^n.$$

  • 局部最小值点：
    大多数优化算法只能找到局部最小值点，即在某个邻域内使目标函数值最小的点。
    点 $x^*$ 称为局部最小值点（或弱局部最小值点），如果存在 $x^*$ 的一个邻域 $\mathcal{N}$，使得

    $$f(x^*) \leq f(x), \quad \forall\, x \in \mathcal{N}.$$

  • 严格局部最小值点：
    若存在邻域 $\mathcal{N}$，使得

    $$f(x^*) < f(x), \quad \forall\, x \in \mathcal{N},\; x \neq x^*,$$

    则称 $x^*$ 为严格局部最小值点。

    

• 识别一个局部最小

  • 当目标函数 $f$ 光滑时，有多种高效且实用的方法可用于识别局部极小值点。

  • 特别地，若 $f$ 二阶连续可微，则可通过考察以下两个量来判断某点 $x^*$ 是否为局部极小值点（甚至严格局部极小值点）：

    • 梯度 $\nabla f(x^*)$
    • Hessian 矩阵 $\nabla^2 f(x^*)$

  • 一阶必要条件

    • 若 $x^*$ 是函数 $f$ 的局部极小值点，且 $f$ 在 $x^*$ 的某个开邻域内连续可微，则必有

      $$\nabla f(x^*) = 0.$$

      此条件称为一阶必要条件（first-order necessary condition）。
    • 若 $\nabla f(x^*) = 0$，则称 $x^*$ 为函数 $f$ 的驻点（或平稳点，stationary point）。
    • 因此，任何局部极小值点都必须是驻点。

  • 二阶必要条件

    • 若 $x^*$ 是函数 $f$ 的局部极小值点，且 Hessian 矩阵 $\nabla^2 f$ 在 $x^*$ 的某个开邻域内连续，则必有：
      • 梯度为零：$\nabla f(x^*) = 0$，
      • Hessian 矩阵半正定：$\nabla^2 f(x^*) \succeq 0$。

    这两个条件合称为二阶必要条件（second-order necessary conditions）。

  • 二阶充分条件

    • 假设 $\nabla^2 f$ 在点 $x^*$ 的某个开邻域内连续，且满足

    $$\nabla f(x^*) = 0, \quad \nabla^2 f(x^*) \succ 0 \quad \text{（即 Hessian 矩阵正定）},$$

    则 $x^*$ 是函数 $f$ 的严格局部极小值点。

    此为二阶充分条件（second-order sufficient condition）。

  • 针对凸函数的情况

    • 若 $f$ 是凸函数，则其任意局部极小值点 $x^*$ 必为全局极小值点。
    • 进一步，若 $f$ 可微，则任意驻点（即满足 $\nabla f(x^*) = 0$ 的点）$x^*$ 都是 $f$ 的全局极小值点。

• 算法总览
  对于一般的非线性最优化问题，最典型和常见的求解方法是迭代型数值方法。根据迭代过程中下一迭代点的生成方式，这类方法可分为随机搜索型方法和确定型方法。

  • 随机搜索型方法是一类仿生智能优化算法，主要依赖目标函数值信息，不依赖梯度或解析结构。
    它适用于组合优化问题以及规模较小的连续优化问题。
    常见方法包括：遗传算法、模拟退火算法、蚁群优化、神经网络方法等。

  • 确定型方法根据所利用函数信息的程度，进一步分为：

    • 直接搜索法（又称模式搜索法）
    • 梯度型方法

  • 直接搜索法通过观察目标函数值的变化规律来探测下降方向，并沿该方向寻找更优解。
    它不需要计算梯度，适用于以下情形：

    • 变量维数较低，
    • 约束结构简单，
    • 目标函数形式复杂或不可导，导致梯度难以获取或计算成本高。
      典型算法包括：坐标轮换法、Hooke-Jeeves 方法、Powell 共轭方向法等。

• 两种策略
  对于梯度型数值方法(Gradient-based),一般通过两种策略，来
  由当前迭代点产生下一选代点：线搜索策略和 信赖域策略。

  • 线搜索
    • 在线搜索策略（line search）中，算法首先选择一个搜索方向 $p_k$，然后从当前迭代点 $x_k$ 出发，沿该方向寻找一个函数值更低的新迭代点。
    • 沿方向 $p_k$ 移动的步长 $\alpha > 0$ 通常通过近似求解如下一维优化问题来确定：

      $$\min_{\alpha > 0} f(x_k + \alpha p_k).$$

    • 虽然精确求解该一维问题能最大程度地利用方向 $p_k$ 的下降潜力，但精确线搜索计算代价高且通常不必要。因此，实际算法多采用满足一定条件（如 Wolfe 条件）的非精确线搜索。
  • 信赖域
    • 在信赖域策略（trust region method）中，算法利用当前已知的关于目标函数 $f$ 的信息，构造一个模型函数 $m_k$，使其在当前迭代点 $x_k$ 附近的行为与真实的 $f$ 相似。
    • 然而，当 $x$ 远离 $x_k$ 时，模型 $m_k$ 可能不再是对 $f$ 的良好近似。
    • 因此，该策略将对模型函数的最小化限制在 $x_k$ 周围的一个信赖域内，即求解如下子问题：

    $$\begin{aligned} \min_{p} \quad & m_k(x_k + p) \\ \text{s.t.} \quad & \|p\|_2 \leq \Delta_k, \end{aligned}$$

    其中 $\Delta_k > 0$ 是当前信赖域的半径，用于控制搜索范围。
    • 模型函数 $m_k$ 通常取为二次函数，形式如下：

      $$m_k(x_k + p) = f_k + p^T \nabla f_k + \frac{1}{2} p^T B_k p,$$

      其中：
      • $f_k = f(x_k)$，
      • $\nabla f_k = \nabla f(x_k)$ 是目标函数在 $x_k$ 处的梯度，
      • $B_k$ 是 Hessian 矩阵 $\nabla^2 f(x_k)$ 或其某种近似（如拟牛顿法中的近似）。
  • 线搜索VS信赖域

    • 线搜索（Line Search）与信赖域（Trust Region）方法的核心区别在于确定方向与步长的顺序不同。

    • 线搜索方法：

      • 首先选定一个搜索方向 $p_k$；
      • 然后在该方向上确定一个合适的步长 $\alpha_k > 0$，使得新点 $x_{k+1} = x_k + \alpha_k p_k$ 能有效降低目标函数值。

    • 信赖域方法：

      • 首先设定一个最大移动距离，即信赖域半径 $\Delta_k > 0$；
      • 然后在球形区域 $\{ p \mid \|p\|_2 \leq \Delta_k \}$ 内同时选择方向和步长（即向量 $p$），以在该约束下尽可能优化模型函数，从而获得最佳改进。

• 线搜索——搜索方向

  • 线搜索算法要求搜索方向 $p_k$ 是一个下降方向（descent direction），即满足

  $$p_k^T \nabla f(x_k) < 0.$$

  • 这一条件保证了：存在某个 $\varepsilon > 0$，使得对所有 $0 < \alpha \leq \varepsilon$，有

  $$f(x_k + \alpha p_k) = f(x_k) + \alpha\, p_k^T \nabla f(x_k) + o(\alpha) < f(x_k),$$

  即沿 $p_k$ 走“足够小”的一步，函数值必定下降。

  • 一旦确定了下降方向，下一步是通过线搜索确定合适的步长 $\alpha_k$。
    通常，这类算法生成的迭代点列 $\{x_k\}$ 对应的目标函数值 $\{f(x_k)\}$ 是单调递减的，因此线搜索方法也被称为下降算法。

  • 在影响算法效率的因素中，搜索方向的选择比步长的精确性更为关键。一个良好的方向往往比精细调整步长更能加速收敛。

  • 搜索方向包括：

    • 最速下降方向：$p_k = -\nabla f(x_k)$
    • 牛顿方向：$p_k = -[\nabla^2 f(x_k)]^{-1} \nabla f(x_k)$
    • 拟牛顿方向：$p_k = -B_k^{-1} \nabla f(x_k)$，其中 $B_k$ 是 Hessian 矩阵的近似

• 最速下降方向

  • 最速下降方向（steepest descent direction）是指在当前点 $x_k$ 处，使目标函数 $f$ 下降最快的方向。

  • 考虑一阶泰勒展开：

  $$f(x_k + \alpha p) = f(x_k) + \alpha\, p^T \nabla f(x_k) + o(\alpha), \quad \alpha > 0.$$

  要使函数值在单位步长下下降最多，应最小化方向导数 $p^T \nabla f(x_k)$，即求解：

  $$\min_{p} \; p^T \nabla f_k \quad \text{subject to} \quad \|p\| = 1.$$

  • 该问题的解为：

  $$p = -\frac{\nabla f_k}{\|\nabla f_k\|},$$

  即负梯度方向是单位长度下的最速下降方向。

  • 因此，最速下降法（又称梯度法或梯度下降法）采用搜索方向：

  $$p_k = -\nabla f(x_k).$$

  

  - 最速下降方向的优点是仅需计算梯度 $\nabla f_k$，无需二阶导数信息。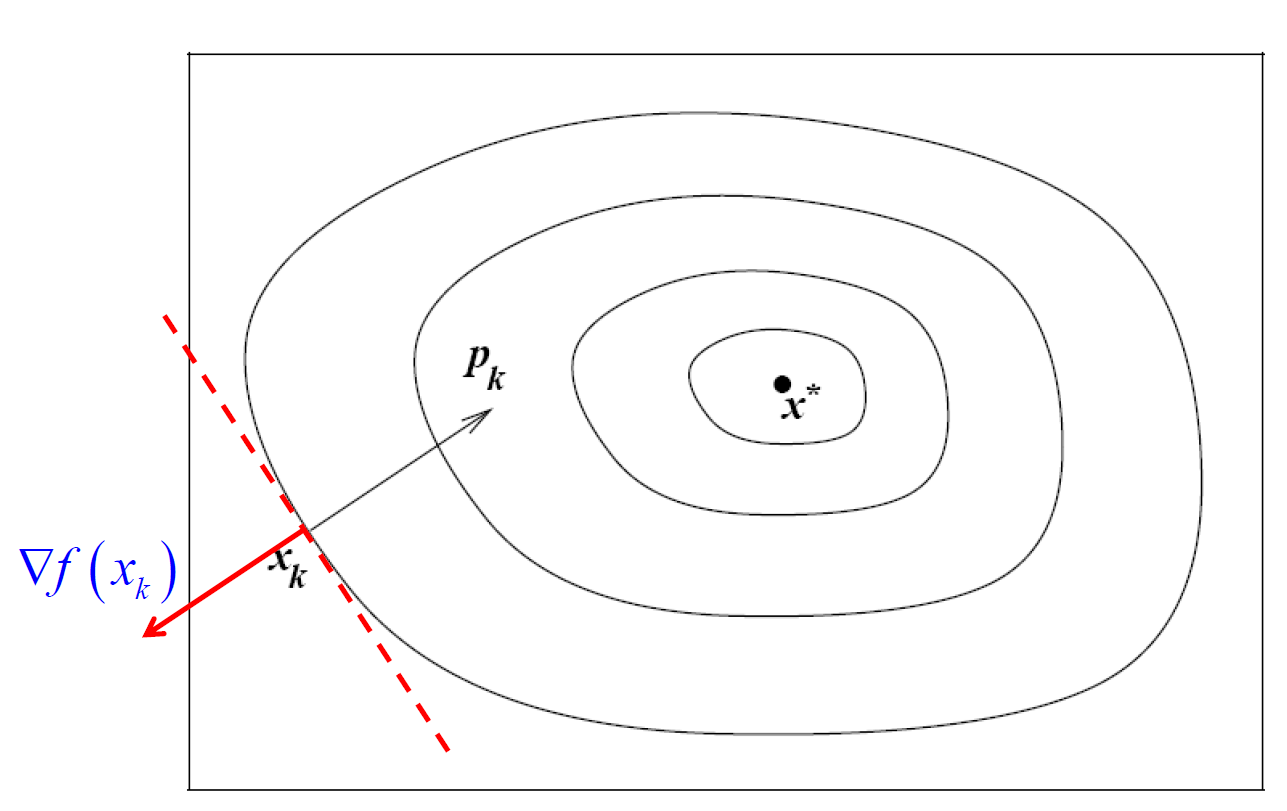
  • 但在困难问题上，其收敛速度可能极其缓慢。
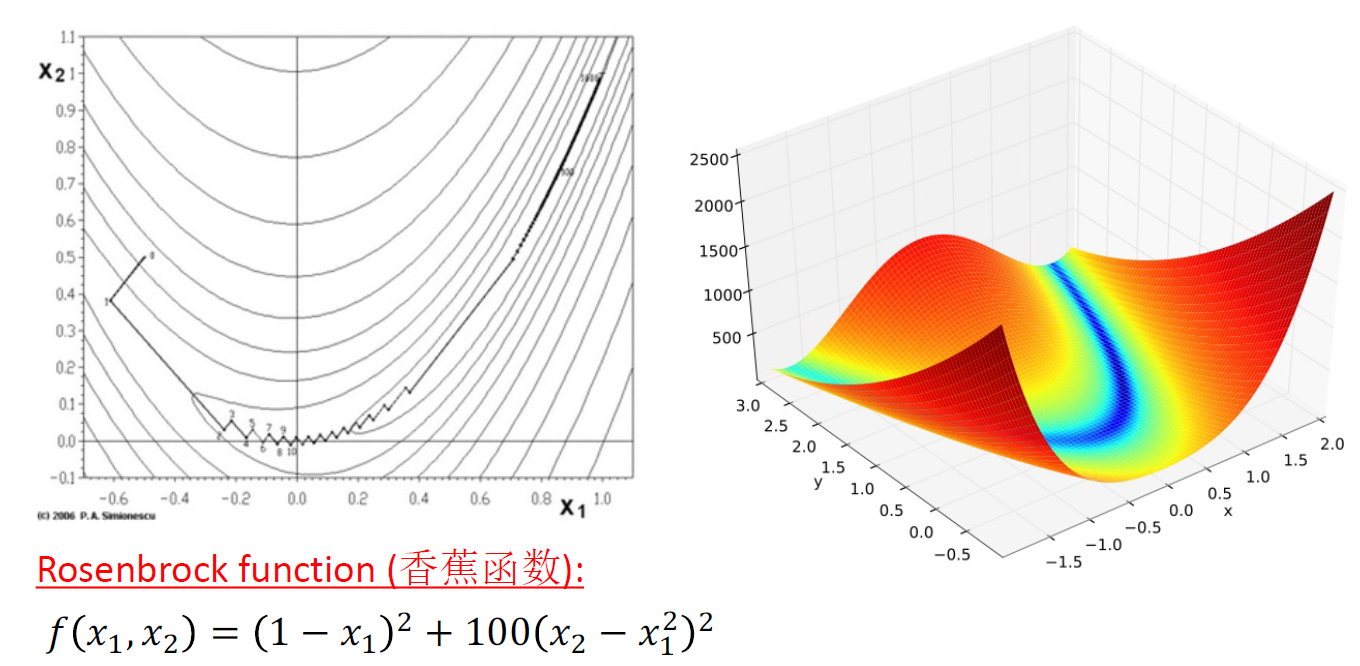